Motion can only be measured relative to an observer; length and time are relative quantities that depend on the observer’s frame of reference.
Some measured quantities of objects travelling at very high speeds cannot be explained by Newtonian physics. Einstein’s Theory of Special Relativity predicts significantly different results to those of Newtonian physics for velocities approaching the speed of light.
The Theory of Special Relativity is based on two postulates. The first postulate is that the laws of physics are the same in all inertial reference frames. The second postulate is that the speed of light in a vacuum is an absolute constant.
In relativistic mechanics, there is no absolute length or time interval.
At relativistic speeds, time intervals in moving frames of reference are dilated when observed from a stationary reference frame according to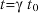 
where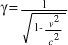 
, is the Lorentz factor, t0 is the time interval in the moving frame of reference and t is the time interval in the stationary observer’s frame of reference.
- Solve problems using 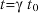and the Lorentz factor formula.
- Explain the effects of time dilation on objects moving at relativistic speeds.
Animation: Relativity (click when it's running)
Video: Red Bull Bike Express
Video: Special Relativity: Crash Course
Video: Twin Paradox
Some subatomic particles exist in the laboratory for very short time periods before decaying. These same particles are detected as part of cosmic ray showers in the atmosphere, travelling at relativistic speeds close to the speed of light.
Time dilation effects allow these particles to travel significant distances without decay.
- Calculate and compare lifetimes and therefore distances travelled by subatomic particles in stationary and moving reference frames.
- Solve problems involving subatomic particles moving at relativistic speeds.
Video: Impossible Muons
An object moving at relativistic speeds is shorter to an observer in a stationary frame of reference, and the length is given by: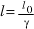 
, where l0 is the length in the moving object’s frame of reference and l is the length in the stationary observer’s frame of reference.
- Solve problems using .
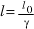- Explain the effects of length contraction on objects moving at relativistic speeds.
Video: Michelson-Morley Experiment
The magnitude of the relativistic momentum of a moving object is given by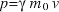 
where m0 is the mass of the object in the frame of reference where the object is stationary and v is the speed of the object.
- Solve problems using
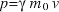
- Explain why masses moving at relativistic speeds are unable to reach the speed of light.
Practice program: Relativity