This uses the concepts of force developed in Stage 1, Subtopic 1.2: Forces and the concept of circular motion in Stage 2, Subtopic 1.3: Circular motion and gravitation

Magnets, magnetic materials, moving charges, and current-carrying conductors experience a force in a magnetic field.

The magnetic force on a moving charged particle within a uniform magnetic field depends on the velocity of the particle, its charge, the magnetic field, and the angle between the velocity and magnetic field.

The force on a current-carrying conductor within a uniform magnetic field depends on the current in the conductor, the length of the conductor within the magnetic field, the magnetic field strength, and the angle between the conductor and magnetic field.

• Determine the direction of one of:
  • force
  • magnetic field
  • charge movement

given the direction of the other two.

• Solve problems involving the use of 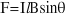 for a current-carrying conductor and  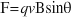for a moving charged particle.

Practice program: Direction of magnetic force on a wire

Video: Magnetic force demonstrations (chapter 8, up to 3:53)

Video: Magnetic force calculations (11:36-34:39)

A charged particle moving at right angles to a uniform magnetic field experiences a force of constant magnitude at right angles to the velocity. The force changes the direction but not the speed of the charged particle, therefore causes centripetal acceleration.

• Explain how the velocity dependence of the magnetic force on a charged particle causes the particle to move with uniform circular motion when it enters a uniform magnetic field at right angles.
• Derive 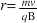 for the radius r of the circular path of an ion of charge q and mass m that is moving with speed v at right angles to a uniform magnetic field of magnitude B.
• Solve problems involving the use of .

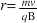Simulation: Charged Particle in a Magnetic Field

Video: Teltron Tube

Video: Explanation of circular motion in magnetic field

Video: Magnetic force calculations (34:42-41:13)

Cyclotrons are used to accelerate ions to high speed. Radioisotopes used in medicine and industry may be produced from collisions between high-speed ions and nuclei.

Video: Isotope Production and Distribution

Video: Medical and Industrial Uses (especially chapter 6)

Videos: Medical Isotope and Cyclotron Facility | Day in the Life Nuclear Medicine

The magnetic field within the dees of a cyclotron causes the charged particles to travel in a circular path, so that they repeatedly pass through the electric field.

• Describe the nature and direction of the magnetic field needed to deflect ions into a circular path in the dees of a cyclotron.
• Derive the formula 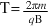 for the period T of the circular motion of an ion, and hence show that the period is independent of the speed of the ion.
• Use  to relate the period to the frequency of the alternating potential differences.
  
• Derive the formula 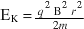or the kinetic energy  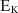of the ions emerging at radius r from a cyclotron.
• Explain why E_K is independent of the potential difference across the dees and, for given ions, depends only on the magnetic field and the radius of the cyclotron.
• Solve problems involving the use of 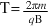 and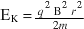

Simulation: Cyclotron

Video: Circular motion in a cyclotron

Video: Magnetic force calculations (41:14-42:58)