This uses the concept of waves developed in the Stage 1, Subtopics 5.1: Wave model and 5.3 Light.
Oscillating charges produce electromagnetic waves of the same frequency as the oscillation; electromagnetic waves cause charges to oscillate at the frequency of the wave.
- Use the frequency of oscillation of the electrons in the transmitting and receiving antennae to explain the transmission and reception of electromagnetic signals.
Electromagnetic waves are transverse waves made up of mutually perpendicular, oscillating electric and magnetic fields.
- Relate the orientation of the receiving antenna to the plane of polarisation of electromagnetic waves.
The speed of a wave, its frequency, and its wavelength are related through the formula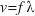 
.
- Solve problems using .
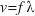Video: Polarisation of light
Video: Disappearing Black Disk
Video: Polarised glasses video
Most light sources emit waves that radiate in all directions away from the source.
Monochromatic light is light composed of a single frequency.
Coherent waves maintain a constant phase relationship with each other.
- Describe what is meant by two wave sources being in phase or out of phase.
- Explain why light from an incandescent source is neither coherent nor monochromatic.
When two or more electromagnetic waves overlap, the resultant electric and magnetic fields at a point can be determined using the principle of superposition.
When the waves at a point are in phase, ‘constructive interference’ occurs.
When the waves at a point are out of phase, ‘destructive interference’ occurs.
- Use the principle of superposition to describe and represent constructive and destructive interference.
For two monochromatic sources in phase, the waves at a point some distance away in a vacuum:
- constructively interfere when the path difference from the sources to the point is
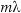
- destructively interfere when the path difference from the sources to the point is
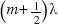
where m is an integer and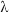 
is the wavelength.
- Use the principle of superposition to determine points of maximum or minimum amplitude resulting from the interference of light from two wave sources of the same frequency.
- Use constructive and destructive interference to explain the maximum and minimum amplitudes.
Path difference/overlapping waves: Sheet | Explanation and questions
Simulation: Interference of Waves (water, sound, light)
Young’s double-slit experiment can be used to demonstrate the wave behaviour of light.
The formulae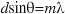 
and 
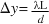can be used to analyse the interference pattern, where d is the distance between the slits, 
is the angular position of the maximum,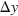 
is the distance between adjacent minima or maxima on the screen, and L is the slit-to-screen distance.
- Describe how two-slit interference is produced in the laboratory using a coherent light source or using a single slit between a light source and the double slit.
- Describe how diffraction of the light by the slits in a two-slit interference apparatus allows the light to overlap and hence interfere.
- Sketch a graph of the intensity distribution for two-slit interference of monochromatic light. (Consider only cases where the slit separation is much greater than the width of the slits.)
- Explain the bright fringes of a two-slit interference pattern using constructive interference, and the dark fringes using destructive interference.
- Solve problems involving the use of 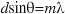and .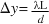
- Determine the wavelength of monochromatic light from measurements of the two-slit interference pattern.
The interference pattern produced by light passing through a transmission diffraction grating demonstrates the wave behaviour of light.
Transmission diffraction gratings can be used to analyse the spectra of various light sources.
The formula 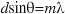can be used to analyse the interference pattern.
- Describe how diffraction by the very thin slits in a grating allows the light from the slits to overlap and hence interfere to produce significant intensity maxima at large angles.
- Derive 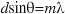for the intensity maxima in the pattern produced by a transmission diffraction grating, where d is the distance between the slits in the grating and is the angular position of the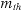
maximum (m specifies the order of the maximum). - Solve problems involving the use of .
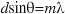- Sketch a graph of the intensity distribution of the maxima produced by a grating, for monochromatic light.
- Determine, from the distance between the slits in the grating, the maximum number of orders possible for a given grating and wavelength.
- Describe how a grating can be used to measure the wavelength of light from a monochromatic source.
- Describe and explain the white-light pattern produced by a grating.
- Identify the properties of a grating that make it useful in spectroscopy.