This uses the concepts of acceleration and force developed in Stage 1, Subtopic 1.1: Motion under constant acceleration and 1.2: Forces.

Centripetal acceleration occurs when the acceleration of an object is perpendicular to the velocity of the of the object. An object that experiences centripetal acceleration undergoes uniform circular motion. The centripetal acceleration is directed towards the centre of the circular path.

The magnitude of the centripetal acceleration is constant for a given speed and radius and given by .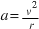

The formula 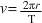 relates the speed, v, to the period, T, for an object undergoing circular motion with radius, r.

• Solve problems involving the use of the formulae 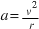,  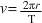 and .
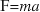• Use vector subtraction to show that the change in the velocity, and hence the acceleration, of an object over a very small time interval is directed towards the centre of the circular path.

Spacecraft Simulation (or Construct capx)

On a flat curve, the friction force between the tyres and the road causes the centripetal acceleration. To improve safety, some roads are banked at an angle above the horizontal.

• Draw a diagram showing the force vectors (and their components) for a vehicle travelling around a flat curve and around a banked curve.
• Explain how a banked curve reduces the reliance on friction to provide centripetal acceleration.

Real world example: Nardo Ring (Italy)

Simulations: Banking Angle | TrackMania track file

Derivation of the Banking Angle Formula: Video | Whiteboard scribbles | Angle proof

Objects with mass produce a gravitational field in the space that surrounds them.

An object with mass experiences a gravitational force when it is within the gravitational field of another mass.

Gravitational field strength, g, is defined as the net force per unit mass at a particular point in the field.

This definition is expressed quantitatively as 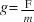 hence it is equal to the acceleration due to gravity. The magnitude of the acceleration due to gravity at the surface of the Earth is 9.80 m s^–2.

• Explain that the acceleration of a projectile is always downwards and independent of its mass.

All objects with mass attract one another with a gravitational force; the magnitude of this force can be calculated using Newton’s law of universal gravitation.

Every particle in the universe attracts every other particle with a force that is directly proportional to the product of the two masses and inversely proportional to the square of the distance between them.

The force between two masses, m₁ and m₂, separated by distance, r, is given by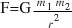

• Solve problems using Newton’s Universal Law of Gravitation.
• Use proportionality to discuss changes in the magnitude of the gravitational force on each of the masses as a result of a change in one or both of the masses and/or a change in the distance between them.
• Explain that the gravitational forces are consistent with Newton’s Third Law.
• Use Newton’s Law of Universal Gravitation and Second Law of Motion to calculate the value of the acceleration due to gravity, g, on a planet or moon.

Video: Bending spacetime

Video: Which Way Is Down? (up to 14:50)

Simulations: Gravity Force Lab | Gravity Simulator

Tool: Satellite Map

Many satellites orbit the Earth in circular orbits.

• Explain why the centres of the circular orbits of Earth satellites must coincide with the centre of the Earth.
• Explain that the speed, and hence the period, of a satellite moving in a circular orbit depends only on the radius of the orbit and the mass of the central body (m₂) about which the satellite is orbiting and not on the mass of the satellite.
• Derive the formula 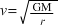 for the speed, v, of a satellite moving in a circular orbit of radius, r, about a spherically symmetric mass, M, given that its gravitational effects are the same as if all its mass were located at its centre.

Simulation: Gravity and Orbits

Kepler’s Laws of Planetary Motion describe the motion of planets, their moons, and other satellites.

Kepler’s First Law of planetary motion: All planets move in elliptical orbits with the Sun at one focus.

Kepler’s Second Law of Planetary Motion: The radius vector drawn from the Sun to a planet sweeps equal areas in equal time intervals.

• Use Kepler’s first two Laws to solve problems involving the motion of comets, planets, moons, and other satellites.

Kepler’s Third Law of Planetary Motion shows that the period of any satellite depends upon the radius of its orbit.

For circular orbits, Kepler’s Third Law can be expressed as: .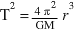

• Derive
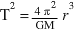
• Solve problems using the mathematical form of Kepler’s Third Law for circular orbits.
• Solve problems involving the use of the formulae 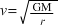,  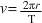and .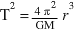
• Explain why a satellite in a geostationary orbit must have an orbit in the Earth’s equatorial plane, with a relatively large radius and in the same direction as the Earth’s rotation.
• Explain the differences between polar, geostationary, and equatorial orbits. Justify the use of each orbit for different applications.
• Perform calculations involving orbital periods, radii, altitudes above the surface, and speeds of satellites, including examples that involve the orbits of geostationary satellites.

Video: Gravity and Kepler's Laws

Simulations: Kepler's Laws | Satellites