This uses the concepts of force developed in Stage 1, Subtopic 1.2: Forces and energy in Stage 1, Subtopic 4.1: Energy.
The electric potential difference, 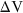 , between two points is the work done per unit charge on a small positive test charge moved between the points, provided that all other charges remain undisturbed.
, between two points is the work done per unit charge on a small positive test charge moved between the points, provided that all other charges remain undisturbed.
The electronvolt (eV) is a unit of measurement which describes the energy carried by a particle. It is the work done when an electron moves through a potential difference of 1 volt.
- Solve problems involving the use of
 .
. - Convert energy from joules into electronvolts and vice versa.
The magnitude of the electric field (away from the edges) between two oppositely charged parallel plates a distance d apart, where 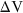 is the potential difference between the plates, is given by the formula:
is the potential difference between the plates, is given by the formula: 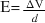 .
.
- Solve problems involving the use of
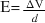 .
.
Video: Electric Field of Parallel Plates (uses 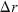 instead of d)
instead of d)
Simulation: Capacitor Lab
The force on a charged particle moving in a uniform electric field is constant in magnitude and direction, thus producing a constant acceleration.
- Derive the formula
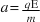 for the acceleration of a charged particle in an electric field.
for the acceleration of a charged particle in an electric field. - Solve problems using
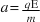 and the motion formulae for the movement of charged particles parallel or antiparallel to a uniform electric field.
and the motion formulae for the movement of charged particles parallel or antiparallel to a uniform electric field. - Describe the motion of charged particles parallel or antiparallel to a uniform electric field.
Video: Example question (for displacement uses  instead of s)
instead of s)
Practice: Motion of charged particles in electric fields (choose Initial velocity parallel to electric field)
In a cyclotron, the electric field in the gap between the dees increases the speed of the charged particles.
- Describe how an electric field between the dees can transfer energy to an ion passing between them.
- Describe how ions could be accelerated to high energies if they could be made to repeatedly move across an electric field.
- Calculate the energy transferred to an ion each time it passes between the dees.
- Explain why the ions do not gain kinetic energy when inside the dees.
A charged particle moving at an angle to a uniform electric field experiences a force which affects both components of its velocity differently. The component of the velocity parallel to the electric field changes due the electric force and the component perpendicular to the field remains constant.
- Compare the motion of a projectile in the absence of air resistance with the motion of a charged particle in a uniform electric field.
- Solve problems for the motion of charged particles that enter a uniform electric field perpendicular to the field.
- Solve problems for the motion of charged particles that enter a uniform electric field at an angle to the field where the displacement of the charged particle parallel to the field is zero.
Simulation: Charged Particle in an Electric Field
